ScienceDirect - Компьютеры & Исследование Операций: запрещённый алгоритм поиска для маршрутизации и полной проблемы назначения в компьютерных сетях

Jian Shen ^,^a, Fuyong Xu^a и Peng Zheng^b

^Школа Информатики и Разработки, Университета Ланьчжоу, Ланьчжоу 730000, связь с общественностью Китай
^b Отдел Электрических и Компьютерная Разработка, Университет Калифорнии, Irvine, Калифорнии 92697, США

Доступный онлайн 9 июня 2004.

1. Введение

Сетевой дизайн - фундаментальная проблема с большими возможностями приложений, которые дали начало многим различным моделям и подходам решения [1 и 2]. Общая сетевая проблема дизайна вовлекает минимизацию функции цели стоимости по большому количеству переменных дизайна, таких как мощности ссылки, назначение потока, сетевая топология, местоположения узла, дисциплина приоритета сообщения. Объединенной проблемой маршрутизации и полного назначения, также известного как способность и назначение потока (CFA) проблема, является специальный выпуск общей сетевой проблемы дизайна.

Проблему CFA сначала рассмотрел Gerla в его тезисе [3]. Fratta и др. [4] предложил модель, чтобы свернуть скупую сетевую задержку в случае общей раздвоенной маршрутизации и линейных затрат дизайна, позволяя приложение алгоритма отклонения потока решить соответствующую выпуклую мультитоварную проблему потока. Нанограмм и Hoang [5] исследовали особый случай маршрутизации и полной проблемы назначения, в которой m-M/M/1 стоящая в очереди структура привыкла к образцовым параллельным линиям передачи. Они сформулировали проблему, используя непрерывные полные переменные ссылки, и использовали метод отклонения потока для решения. LeBlanc и Simmons [6] сформулировали маршрутизацию и полную проблему назначения, используя непрерывные полные переменные ссылки и предложили новую выпуклую функцию задержки, отличающуюся от традиционного M/M/1. Gavish и Neuman [7] предложили модель, чтобы совместно свернуть задержку и полные затраты в случае нераздвоенной маршрутизации и дискретных полных функций. Модель была решена, используя процедуру расслабления Lagrangean. Gavish и Altinkemer [8] расширяли работу в [7], рассматривая все возможные маршруты для каждой пары узла сообщения. Они включали ограничения вырезки, которые избыточны в оригинальной проблеме улучшить более низкие границы и предложили интересное эвристическое, чтобы произвести выполнимое решение. Amiri и Pirkul [9] развивали новое смешанное целое число нелинейная программная формулировка для проблемы CFA, используя расслабление Lagrangean и методики оптимизации подградиента и две фазы эвристическая процедура решения, чтобы получить более низкие границы так же как выполнимые решения. Модель преодолела недостаток предыдущих методов. Результаты были по сравнению с теми, о которых сообщают в [8]. Amiri [10] представил новую математическую программную модель, которая включает ограничение, которое устанавливает верхний предел, в среднем связывают стоящую в очереди задержку сети, и рассматривал все возможные маршруты для каждой пары узла сообщения. Amiri и Pirkul [11] развивали модель в [10] с условиями трафика мультичаса наибольшей нагрузки. Mahey и др. [12] продуманные дискретные мощности и функция стоимости комбинируют инсталляционную стоимость с мерой качества обслуживания (Qos) получающейся сети для данного трафика, и предложили смешанное целое число нелинейная модель объединенной способности и проблемы назначения потока, решенной обобщенным методом разложения Клещей. Queiroz и младший [13] предложил эвристический метод для непрерывной способности и проблемы назначения потока, перефразируя проблему в контексте вогнутого программирования и обеспечения альтернативной формулировки спроектированного попарного мультитоварного многогранника потока. Ключевая идея состоит в том, чтобы использовать местные минимумы, чтобы определить вырезки вогнутости, таким образом избегая циклической работы и явного перечисления вершин.

Несколько авторов включили ограничения надежности в проблему CFA. Monma и Sheng [14] представили глобальный сетевой дизайн и модель анализа, чтобы проанализировать сетевую работу в дешевых базовых сетях коммутации пакетов. Lim [15] предложил оптимальную процедуру для того, чтобы свернуть полную стоимость ссылки общего канала, сообщающего о сети при объединенной работе и ограничениях надежности. Ал-Rumaih и др. [16] предложил методологию для сетевого дизайна топологии, рассматривая проблемы единственной ссылки и терпимости отказов узла. Их метод основан на систематических топологических модификациях начальной сети, созданной без требований надежности, но для которого мощности ссылки удовлетворяют ряд ссылки и требований работы пути. Chamberland и Sanso [17] представили модель, чтобы принять во внимание отказы в проблеме CFA. Модель обеспечивает способ оценить обмен между увеличивающейся способностью и более низкой работой в случае отказов. Два различных алгоритма, соответствуя двум различным уровням параллелизма, были предложены и осуществлены.

Предыдущие методы, однако, являются всеми традиционными математическими программными методиками с высоким сложным процессом вычисления. Результатами, произведенными этими методами, являются местные оптимальные решения вместо глобальных оптимальных.

В последние годы, новый запрещённый поиск (TS) metaheuristic алгоритм был быстро развит. Это было введено Перчаточником [18, 19 и 20], и успешно применялось, чтобы решить проблемы, такие как граф, красящий [21], проблема продавца путешествия [22], магазин потока, упорядочивающий [23], цех, намечая [24], и много других комбинаторных проблем оптимизации [25 и 26]. В области телекоммуникаций Laguna и Перчаточник [27] обсуждали развитие метода TS для пропускной способности, упаковывающей проблему. Costamagna и др. [28] представил алгоритм TS для топологической оптимизации широкополосных сетей коммуникации. Chamberland и Sanso [29] представили запрещённый алгоритм поиска для топологического расширения многократно-кольцевых столичных сетей области. Berger и др. [30] просил TS о сети, загружающей проблему многократными средствами. Shyur и Жировик [31] развивали простой TS для того, чтобы оптимизировать систему виртуальных путей в сети ATM. Youngho и др. [32] развитый эффективная процедура TS, чтобы обеспечить плотные верхние границы для волокна, направляющего проблему, являющуюся результатом дизайна оптических транспортных сетей.

Достигнутый успех TS во всех приложениях происходит из-за его выполнения как проблемно-ориентированный. Для каждого выполнения это нуждается в специфических определениях структурных элементов и параметров. Чтобы изучить работу TS, простой алгоритм TS для классической проблемы CFA предложен в этой газете. Действия алгоритма по сравнению с традиционными методиками, и обширные тесты сделаны определить соответствующие значения параметра для алгоритма TS.

Остаток от бумаги организован следующим образом. В Разделе 2, сформулирована проблема CFA. Раздел 3 описывает алгоритм TS для проблемы CFA. Результаты вычислительных экспериментов представлены в Разделе 4. Наконец мы заключаем и предлагаем дальнейшее исследование в Разделе 5.

2. Формулировка проблемы

Классическая маршрутизация и полная проблема назначения могут быть описаны следующим образом: учитывая основную топологию и матрицу требования, как одновременно выбрать мощности ссылки и маршруты, используемые узлами в сети, чтобы гарантировать приемлемый уровень работы по минимальной стоимости [7, 8 и 9]. Эта проблема - сложное нелинейное программирование, у которого есть много сдержанных условий, и она, как известно, NP-законченность [33, 34, 35 и 36].

Чтобы сформулировать классическую проблему CFA, мы делаем те же самые предположения используемыми в [7, 8 и 9]. Предполагается, что сетевая топология, организация очереди и полная структура стоимости, и требования трафика между каждой парой общающихся узлов даны. Мы также предполагаем, что у узлов есть бесконечные буфера, чтобы хранить сообщения, ждущие передачи на ссылках, что процесс прибытия сообщения к сети следует за распределением Пуассона, и те длины сообщения следуют за показательным распределением. Мы далее предполагаем, что задержка распространения ссылок незначительна, что нет никакого сообщения, обрабатывающего задержку в узлах, и есть только единственный класс обслуживания для каждой пары узла сообщения. Согласно этим предположениям, компьютерная сеть смоделирована как сеть независимой очереди M/M/1 [37 и 38], в котором ссылки обработаны как серверы с сервисными нормами, пропорциональными мощностям ссылки. Клиенты - сообщения, области ожидания которых - сетевые узлы.

Мы используем следующее примечание:

Объективная функция должна свернуть общую стоимость сети, данной по выражению в Eq. (1). Первый срок объективной функции указывает общую стоимость задержки. Второй термин относится к полным фиксированным расходам, вычисленным как сумма начальной стоимости установки и стоимости расстояния. Третий срок - переменная стоимость, связанная со ссылками в сети. Ограничение (2) гарантии выполнимость потока на каждой ссылке в терминах способности, назначенной на это. Ограничения ((3) и (4)) гарантируют, что только один маршрут для каждой пары адресата происхождения и только один тип линии выбраны для каждой ссылки, соответственно.

3. Табу ищет CFA

Запрещённый поиск - процедура, используя идеи от искусственного интеллекта, который ведет местные методы поиска, чтобы преодолеть местный optimality и получить оптимальный или около оптимальных решений для твердых комбинаторных проблем оптимизации. Начинаясь с начального решения, метод исследует место решения, двигаясь от решения до лучшего решения по соседству при каждой итерации. Это позволяет методу сбегать из местного оптимума и исследовать другие области места поиска, но качество решения может ухудшиться от одной итерации до следующего, какие отличные TS формируют классические местные методы поиска. Чтобы избежать циклически повторять, особенно проектированный механизм памяти, известный как запрещённый список, используется, чтобы хранить ранее посещаемые решения или определенные признаки их, которые не будут полностью изменены для определенного числа итераций. В частности состояние запрещённого перемещения может быть отвергнуто и сделать доступным сразу же, если определенный критерий стремления встречен. Для более всестороннего описания TS читатели могут обратиться к [25].

Так как TS по сравнению с традиционными методиками в этой газете, мы предлагаем простой алгоритм TS для проблемы CFA, и фундаментальные компоненты процедуры определены в следующем.

3.1. Представление решения

Общающейся паре узла адресата происхождения p, p 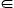Π, есть |S_p | маршруты кандидата, среди которых и только один отобраны, чтобы направить соответствующий трафик. Используя составной переменный армированный пластик, чтобы представить индекс маршрута, мы доберемся | Π | такие переменные все вместе, каждый представляя определенный маршрут для пары узла. Вектор маршрута r = (r₀, r₁, Λ, r _{| Π | − 1}) может быть получен, если мы помещаем весь | Π | переменные вместе, для 0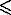r_p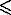|S_p | − 1. К ссылке l, l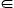L, есть |I_l | полные типы кандидата, среди которых только один назначен на линию. Используя составную переменную статью, чтобы представить индекс полных типов. Мы получим |L | такая переменная все вместе, каждый представляя способность печатает для линии. Полный вектор c = (c₀, c₁, Λc_{|L | − 1}) может быть получен, если мы помещаем весь |L | переменные вместе, для 0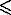c_l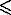|I_l | − 1. Естественно для нас использовать эти два вектора, чтобы представить решение CFA.

3.2. Начальное решение

Обычно есть преимущества для старта с начального решения, которое имеет высокое качество. Мы изучаем следующие методы для проблемы CFA.

3.2.1. Начальный выбор маршрута

Мы используем четыре метода маршрута следующим образом:

Случайный метод маршрута (RRM): Каждый раз перед началами процедуры TS, программа используется, чтобы произвести | Π | случайные целые числа, которые лежат в интервале [0, |S_p | − 1]. Позвольте компонентам маршрута направлять r равный те случайные цифры соответственно, таким образом начальное решение для маршрута могло быть достигнуто.

Самый короткий метод маршрута (SRM): Для каждой пары узла сообщения, выберите самый короткий маршрут из его набора маршрута кандидата, чтобы нести соответствующий трафик.

Минимум прыгает через метод (MHM): перелет маршрута определен как число узлов (или ссылки), это пересекает. Этот метод должен выбрать тот с минимальными перелетами от набора маршрута кандидата для каждой пары узла сообщения.

Самый длинный метод маршрута (LRM): Для каждой пары узла сообщения, выберите самый длинный маршрут из его набора маршрута кандидата, чтобы нести соответствующий трафик.

3.2.2. Начальное полное назначение

Много методов могут также быть применены к полному назначению. В этой газете мы только принимаем лучший полный метод назначения. Если маршруты всех пар узла сообщения были отобраны, поток каждой ссылки также решен. В полном наборе кандидата должно быть лучшее полное значение кандидата, которое может сделать общую стоимость сети, минимум. Мы можем найти эти полные значения, и назначить на ссылки.

3.3. Переместите определение

Два вида перемещений определены только, чтобы направить решение, то есть, М. ₊ и М. ₋. Прежний может привести к предварительному решению r_t=r_c+e_i, и последнему, r_t=r_c−e_i. Поскольку e_i - идентичный вектор, и реальный масштаб времени и дистанционное управление представляют решение для испытания и текущее решение, соответственно. Очевидно, те два перемещения удовлетворяют условие 'законченности', то есть, любое решение, везде, где это находится в месте решения, может быть достигнуто от другого решения до определенного числа таких перемещений.

3.4. Запрещённый список

Список (рис. 1) используется, чтобы сформировать запрещённый список. Каждый модуль в списке состоит из двух частей, то есть, индекс общающейся пары узла, которая колеблется от 0 до | Π | −1, и операции, наложенные на это, которое представлено или 0 или 1, где 0 обращается к М. ₊ и 1 к М. ₋. Например, модуль, содержащий (10,0) средства, что перемещение запрещено, если это приводит к r_t=r_c+e₁₀. Запрещённый список работает, поскольку "сначала в первом" (в порядке поступления) располагает в стеке. Во время процедуры поиска новое запрещённое перемещение добавлено в конце списка, и самое старое перемещение удалено из головки списка.

Рис. 1. Структура запрещённого списка.

Длина списка - запрещённый размер списка (T_max). Запрещённый размер списка представляет число итераций, которые перемещение остается табу, препятствуя поиску циклически повторить. Когда запрещённый список короток, запрещённые перемещения, позволяют быть полностью измененными после немногих итераций, который заставляет поиск подчеркнуть интенсификацию. Если запрещённый список длинен, много перемещений - табу, и поиск вызван в области, которые еще не посещались, который заставляет поиск сосредоточиться на разнообразии. Таким образом размер запрещённого списка должен зависеть от размера и характеристик проблемы, предложенной Перчаточником [25]. В экспериментах мы исследуем различные значения запрещённых размеров списка.

3.5. Стратегия поиска соседства

Стратегия поиска соседства определяет, которые двигаются по соседству, выбран при каждой итерации. Это очень важно по качеству решения и эффективности поиска. Следующие три метода проверены.

Лучший метод (BM): Произведите и оцените все решения по соседству текущего решения. Выберите перемещение, приводящее к решению с лучшим значением функции возражения как следующее перемещение. Отметьте, что, если перемещение - табу, лучшее незапрещённое перемещение отобрано.

Первый метод (ИЗ): Произведите последовательно набор решений по соседству текущего решения. Выберите первое перемещение, идентифицированное как приведение к решению с улучшенным объективным функциональным значением. Если никакое улучшающееся перемещение не существует, выберите лучшее незапрещённое перемещение.

Типовой метод (СМ): При условиях, где размер соседства является очень большим, это является отнимающим много времени, чтобы искать на целом соседстве. Типовой метод беспорядочно производит подмножество соседства текущего решения. Все решения в этом подмножестве получены и оценены, и перемещение, приводящее к лучшему объективному функциональному значению, выбрано как следующее перемещение. Если перемещение - табу, лучшее незапрещённое перемещение в подмножестве отобрано.

3.6. Критерий стремления

По сравнению с эффектом ограничения запрещённых ограничений критерии стремления делают процесс поиска бесплатным. Критерий стремления проектирован, чтобы отвергнуть запрещённое состояние и сделать перемещение кандидата в запрещённом состоянии допустимым. В этой статье используется следующий критерий стремления: если перемещение дает лучшее объективное функциональное значение чем лучшее, найденное пока, то оно может быть взято как следующее перемещение несмотря на его запрещённое состояние.

3.7. Остановка критерия

Много останавливающихся критериев могут быть развиты в зависимости от природы изучаемой проблемы. Самый общий критерий, который используется в этой газете, является максимальным числом итераций.

3.8. Объективная функция

Объективная функция проблемы CFA дана в Eq. (1). Однако, во многих случаях, трудно искать выполнимое решение, или потребуется большое количество времени, чтобы искать такой, который удовлетворяет упомянутые выше ограничения. Таким образом мы переопределяем объективную функцию для проблемы CFA следующим образом:

где, C - большая, положительная константа, которая является 1×10⁵ в этой газете. Делая так, мы можем передать принужденную проблему оптимизации в эквивалентную непринужденную проблему, которая удобна практически.

3.9. Запрещённая процедура поиска

Основанный на предыдущем обсуждении, мы представляем процедуру TS для проблемы CFA.

Шаг 1. Инициализация: Произведите начальное решение (r₀, c₀) согласно отобранному начальному методу, и вычислите общую стоимость Z (r₀, c₀); Инициализируйте текущее решение (дистанционное управление, c_c) и лучшее решение (r_b, центибар), устанавливая (r_c=r₀, c_c=c₀) и (r_b=r₀, c_b=r₀), соответственно; инициализируйте настраивающиеся параметры.
Шаг 2. Поиск соседства (СМ):

(1) Произведите подмножество соседства М., и все решения в М. получены.
(2) Оцените решения: Позвольте (r_tb, c_tb) быть лучшим решением для Z (r_tb, c_tb) минимально в М. Если перемещение (r_c→r_tb) не является табу, и Z (r_tb, c_tb) <Z (r_b, центибар), пойдите в (3); иначе пойдите в (4). Если перемещение - табу, но переписывающийся Z передает критерий стремления, то есть. Z (r_tb, c_tb) <Z (r_b, центибар), идут в (3); иначе позвольте (r_tb, c_tb) быть решением для Z (r_tb, c_tb) самый близкий минимум в М., повторять этот шаг.
(3) Возобновите лучшее решение: Набор (r_b=r_tb, c_b=c_tb) и Z (r_b, центибар) =Z (r_tb, c_tb).
(4) Двигайтесь: Набор (r_c=r_tb, c_c=c_tb).
(5) Измените запрещённый список: Поместите противоположное перемещение в запрещённый список и удалите самое старое перемещение в этом.
Шаг 3. Проверьте останавливающийся критерий: Если останавливающийся критерий удовлетворен, пойдите, чтобы ступить 4; иначе пойдите, чтобы ступить 2.
Шаг 4. Остановите и сообщите о результатах.

4. Вычислительные результаты

Мы изучили эти четыре топологии, которой показывают в рис. 2, рис. 3, рис. 4 и рис. 5, то есть. ARPA, ОКТЯБРЬ, США и КОЛЬЦО. Эти сети наряду с параметрами трафика и структурой стоимости подобны проверенным в [7, 8 и 9]. Во всех четырех сетях каждый узел общается с любым узлом. В сети ARPA было 420 общающихся пар узла с 4 сообщениями в секунду, посылаемую вдоль выбранного маршрута. Соответствующие значения были 650 и 1 на ОКТЯБРЬ, и 650 и 4 для США, и 992 и 1 для КОЛЬЦА. Набор маршрутов кандидата был получен, используя измененный самый короткий алгоритм пути ранее, и 5 маршрутов были выбраны для каждой пары узла сообщения. Различные мощности, используемые в основном случае и их компонентах стоимости передачи, представлены в Таблице 1. Алгоритм был закодирован на языке C и выполнении на PC с центральным процессором МГц Pentium III-866.

Рис. 2. Топология сети ARPA.

Рис. 3. Топология сети в ОКТЯБРЕ.

Рис. 4. Топология сети США.

Рис. 5. Топология КОЛЬЦЕВОЙ СЕТИ.

Таблица 1. Полный набор ссылки и его компоненты стоимости

Таблица 2 показа результаты с различными длинами сообщения. Чтобы сравнить эффективность нашей процедуры с традиционным методом, мы также сообщаем о результатах, полученных Amiri и Pirkul [9]. Стоимость модуля задержки, как предполагается, составляет 2000 $ в месяц при содействии сообщения для основного случая. И установленные и переменные множители стоимости равны 1. Вычислительные результаты указывают, что и стоившая задержка и повсюду стоят уменьшение по сравнению с результатами в [9]. Чем ниже задерживают стоимость, тем более короткое время ответа пользователям. То есть наш предложенный алгоритм TS получил минимальную общую стоимость и лучшее качество обслуживания в то же самое время. Мы также заметили, что решения немного улучшены в сети ARPA. С увеличением сетевого масштаба у результатов есть существенное усовершенствование. В ОКТЯБРЕ сеть общая стоимость уменьшала 67 %. В сети США это - 59 %, и 61 % в КОЛЬЦЕ. Это может быть заключено от этих результатов, что TS эффективен в решении проблемы CFA, и выше в крупномасштабных сетях.

Таблица 2. Вычислительные результаты с различными длинами сообщения

Чтобы осуществить предложенный алгоритм эффективно, свойства ключевых запрещённых параметров исследованы.

Рис. 6 показывает результатам с различными методами, используемыми, чтобы произвести начальное решение. Можно заметить, что начальное решение имеет существенный эффект на результаты. Решения SRM и MHM превосходят таковые из RRM и LRM. Есть небольшое различие между SRM и MHM. Это может быть приписано факту, что MHM используется, чтобы выбрать маршрут с минимальными перелетами или ссылками, в результате полный трафик в каждой ссылке легче, и общая стоимость ниже по сравнению с другими методами. Поскольку в большинстве случаев, меньше перелетов означает более короткое расстояние и наоборот, различие между MHM и SRM незначительно. Результаты указывают, что хорошее начальное решение должно быть отобрано, чтобы улучшить качество решений, используя TS. Для проблемы CFA начальное решение должно быть произведено MHM или SRM, который используется для остальной части исследования.

Рис. 6. Результаты с различными начальными методами решения (КОЛЬЦО).

Рис. 7 и рис. 8 показывают эффектам и времена центрального процессора с различными стратегиями поиска соседства. Мы замечаем, что стратегия поиска соседства оказывает существенное влияние на работу процедур TS, особенно когда размер соседства является большим. BM, в большинстве случаев, может привести к лучшим решениям, но с большинством времени вычисления. Решения, полученные СМ, не очень близко к тем BM, со чтобы времена центрального процессора. ИЗ проводит меньше раз центрального процессора чем BM, но он приводит к худшим результатам в каждом случае, делая это неподходящий для процедуры TS. Рассматривая качество решения и эффективность в то же самое время, мы можем сделать вывод, что СМ должен быть отобран с более высоким приоритетом, используя TS. Только при обстоятельствах, где размер соседства является маленьким или время не настолько важно, может BM быть примененным.

Рис. 7. Результаты с различным соседством ищут на стратегиях (КОЛЬЦО).

Рис. 8. Времена центрального процессора с различным соседством ищут на стратегиях (КОЛЬЦО).

Когда СМ используется, как выбрать размер образца соседства другая важная проблема. Результаты с различными размерами образца соседства даны в рис. 9. Очевидно, если типовой размер является слишком маленьким, алгоритм не мог бы найти хорошее решение. Когда типовой размер равен 50 (приблизительно 5 % целого соседства), алгоритм прибывает в оптимальное решение. С увеличением размера решения имеют небольшое усовершенствование, но платят больше вычислительных усилий. Поэтому, 5 % соседства должны быть отобраны как подмножество практически.

Рис. 9. Результаты с различными размерами образца соседства (КОЛЬЦО).

О результатах и времена центрального процессора с различными запрещёнными размерами списка сообщают в рис. 10 и рис. 11, соответственно. Замечено, что запрещённый список с размером 7 предложенное Перчаточником [25] также подходящее для проблемы CFA. Когда запрещённый размер списка является маленьким (<7), алгоритм посещает ту же самую последовательность решений много раз, и заканчивается в местном оптимуме. Когда это является большим (> 7), у результатов есть небольшое усовершенствование с увеличением запрещённого размера списка, но за счет большего количества времени вычисления. Таким образом разумно выбрать 7 как запрещённый размер списка для проблемы CFA.

Рис. 10. Результаты с различными запрещёнными размерами списка (КОЛЬЦО).

Рис. 11. Времена центрального процессора с различными запрещёнными размерами списка (КОЛЬЦО).

Кроме того, среднее число итераций и среднее время центрального процессора и для нашего метода и для метода, предложенного Amiri и Pirkul [9], получено в итоге в Таблице 3. Очевидно, наш алгоритм TS в состоянии сходиться очень быстро к оптимальному решению. Оптимальное решение могло быть найдено при средней итерации 90, который является приблизительно в 3 раза меньше чем метод в [9]. Это - потребность указать, что метод решения, описанный в [9], был написан в Паскале и выполнении на IBM-3081D. Принимая во внимание машинные различия, наш метод все еще быстрее чем традиционные методики. Они далее иллюстрируют высокую производительность метода TS.

Таблица 3. Среднее число итераций и времена центрального процессора

5. Заключения

В этой газете запрещённый поиск metaheuristic алгоритм предложен для классической проблемы CFA в компьютерных сетях. Лучшие результаты получены по сравнению с традиционными методиками, таким образом высокая эффективность метода TS далее проверена. Обширный вычислительный показ экспериментов, которые приспосабливают параметры, очень улучшит эффективность и эффективность процедуры TS. Эти результаты также полезны для других сложных проблем оптимизации работы в компьютерных сетях.

В будущей исследовательской работе будет далее изучена работа метода TS. Расширенная интенсификация и стратегии разнообразия [39], и параллельные, реактивные и гибридные методы TS [40, 41 и 42] должны быть применены, чтобы улучшить качество решений. Кроме того, мы применим метод TS к некоторым новым проблемам оптимизации, возникающим в компьютерных сетях, например, вес, устанавливающий проблему в OSPF маршрутизация [43], и т.д.

Справочная информация

1. М. Minoux, Сетевой синтез и оптимальная сеть проектируют проблемы: модели, методы решения и приложения. Сети 19 (1989), стр 313–360. Резюме-INSPEC | $Order Документ | MathSciNet

2. V. Ahuja. Дизайн и анализ компьютерных сетей коммуникации, McGraw-холма, Нью-Йорка (1982).

3. Gerla М. Дизайн сетей с промежуточным накоплением для компьютерной связи. Докторская диссертация, Университет Калифорнии, Лос-Анджелеса, 1973.

4. L. Fratta, М. Gerla и L. Kleinrock, метод отклонения потока: подход к дизайну системы коммуникаций с промежуточным накоплением. Сети 3 (1973), стр 97–133. Резюме-Compendex | $Order Документ | MathSciNet

5. T. Нанограмм и D. Hoang, Объединенная оптимизация способности и назначения потока в переключенной в пакет системе коммуникаций. ИИЭР Сделки на Связи 35 2 (1987), стр 202–209. Резюме-Compendex | Резюме-INSPEC | $Order Документ

6. L. LeBlanc и R. Simmons, Непрерывные модели для полного дизайна больших переключенных в пакет телекоммуникационных сетей. Журнал ORSA при Вычислении 1 (1989), стр 271–286. Резюме-INSPEC | $Order Документ

7. B. Gavish и я. Neuman, система для маршрутизации и полного назначения в компьютерных сетях коммуникации. ИИЭР Сделки на Связи 37 4 (1989), стр 360–366. Резюме-Compendex | Резюме-INSPEC | $Order Документ | Полный Текст через CrossRef

8. B. Gavish и K. Altinkemer, средства проектирования Базовой сети с экономическими обменами. Журнал ORSA при Вычислении 2 (1990), стр 226–252.

9. A. Amiri и H. Pirkul, Маршрутизация и полное назначение в базовых сетях коммуникации. Компьютеры & Исследование Операций 24 3 (1997), стр 275–287. Резюме | Полный Текст + Ссылки | PDF (955 K)

10. A. Amiri, система для дизайна переключенных в пакет сетей коммуникации с экономическими обменами. Компьютерная Связь 21 (1998), стр 1670–1678.

11. A. Amiri и H. Pirkul, Маршрутизация и полное назначение в базовых сетях коммуникации под временем переменные условия трафика. Европейский Журнал Операционного Исследования 117 (1999), стр 15–29. Резюме | Полный Текст + Ссылки | PDF (222 K)

12. P. Mahey, A. Benchakroun и F. Boyer, Способность и назначение потока сетей передачи данных обобщенным разложением Клещей. Журнал Глобальной Оптимизации 20 (2001), стр 173–193. MathSciNet

13. Queiroz М., младший. CH. Эвристическое для непрерывной способности и назначения потока. Европейский Журнал Операционного Исследования 2003; 146:444–59.

14. C. Monma и D. Sheng, дизайн Базовой сети и анализ работы: методология для сетей пакетной коммутации. ИИЭР Журнал на Отобранных Областях в Связи 4 6 (1986), стр 946–965. Резюме-INSPEC | Резюме-Compendex | $Order Документ | Полный Текст через CrossRef

15. Y. Lim, Стоившая минимумом модель определения размеров для общего канала, сообщающего о сетях при объединенной работе и ограничениях надежности. ИИЭР Журнал на Отобранных Областях в Связи 8 9 (1990), стр 1658–1666. Резюме-Compendex | Резюме-INSPEC | $Order Документ | Полный Текст через CrossRef

16. A. Ал-Rumaih, R. Ahmed, S. Bakry и A. Ал-Dhelaan, методология для сетевой топологии проектирует со ссылкой и терпимостью отказов узла. Международный журнал Сетевого Управления 6 1 (1995), стр 42–64.

17. S. Chamberland и B. Sanso, Последовательные и параллельные подходы, чтобы включить надежность в синтез компьютерных сетей. Журнал Сети и Управления Системами 5 2 (1997), стр 131–157. Резюме-Compendex | Резюме-INSPEC | $Order Документ | Полный Текст через CrossRef

18. F. Перчаточник, Будущие пути для программирования целого числа и ссылок к искусственному интеллекту. Компьютеры & Исследование Операций 19 (1986), стр 533–549. Резюме | Полный Текст + Ссылки | PDF (2265 K) | MathSciNet

19. F. Перчаточник, Запрещённая первая часть поиска. Журнал ORSA при Вычислении 1 3 (1989), стр 190–206. Резюме-INSPEC | $Order Документ

20. F. Перчаточник, Запрещённая вторая часть поиска. Журнал ORSA при Вычислении 2 1 (1990), стр 4–32. Резюме-INSPEC | $Order Документ

21. A. Герц и D. Werra, Используя запрещённые методики поиска для окраски графа. Вычисляя 39 (1987), стр 345–351. Резюме-INSPEC | Резюме-Compendex | $Order Документ | MathSciNet

22. М. Malck, М. Guruswamy и М. Pandya, Последовательный и параллельный моделируемый отжиг и табу ищут на алгоритмах проблему продавца путешествия. Летопись Исследования Операций 21 (1989), стр 59–84.

23. J. Barnses и М. Laguna, Решая многократную машину нагруженная проблема времени потока, используя запрещённый поиск. Сделки IIE 25 (1993), стр 121–128.

24. М. Dell'Amico и М. Trubian, Применение табу ищет на цех, намечая проблему. Летопись Исследования Операций 41 (1993), стр 231–252. Резюме-INSPEC | $Order Документ | Полный Текст через CrossRef

25. F. Перчаточник и М. Laguna. Запрещённый поиск, Kluwer Академические Издатели, Дордрехт (1997).

26. I.H. Osman и Г. Laporte, Metaheuristics: библиография. Летопись Исследования Операций 63 (1996), стр 513–623. Резюме-INSPEC | $Order Документ

27. М. Laguna и F. Перчаточник, упаковка Пропускной способности: запрещённый подход поиска. Наука Управления 39 4 (1993), стр 492–500. Резюме-INSPEC | Резюме-Compendex | $Order Документ

28. E. Costamagna, A. Fanni и Г. Giacinto, запрещённый алгоритм поиска для оптимизации телекоммуникационных сетей. Европейский Журнал Операционного Исследования 106 2–3 (1998), стр 357–372. Резюме | Полный Текст + Ссылки | PDF (1617 K)

29. S. Chamberland и B. Sanso, Топологическое расширение многократно-кольцевых столичных сетей области. Сети 36 4 (2000), стр 210–224. Резюме-INSPEC | $Order Документ

30. D. Berger, B. Gendron и др., Табу ищет сеть, загружающую проблему многократными средствами. Журнал Эвристики 6 (2000), стр 253–267. Резюме-INSPEC | Резюме-Compendex | $Order Документ | Полный Текст через CrossRef

31. C.C. Shyur и U.P. Жировик, Оптимизируя систему виртуальных путей запрещённым поиском. Европейский Журнал Операционного Исследования 129 (2001), стр 650–662. SummaryPlus | Полный Текст + Ссылки | PDF (247 K) | MathSciNet

32. L. Youngho, H. Junghee и K. Kugchang, волокно, направляющее проблему в проектировании оптических транспортных сетей с подразделением длины волны мультиплексные системы. Фотонная Сетевая Связь 5 3 (2003), стр 247–257.

33. B. Gavish и S.L. Hantler, алгоритм для оптимального выбора маршрута в сетях SNA. ИИЭР Сделки на Связи 31 10 (1983), стр 1154–1161. Резюме-Compendex | $Order Документ | Полный Текст через CrossRef

34. S. Narasimhan, H. Pirkul и P. De, выбор Маршрута в базовых сетях передачи данных. Компьютерные Сети и Системы цифровой сети комплексного обслуживания 15 (1988), стр 121–133. Резюме | Полный Текст + Ссылки | PDF (961 K)

35. B. Gavish и H. Pirkul, Эффективные алгоритмы для того, чтобы решить ноль мультиограничения проблемы ранца к optimality. Математическое Программирование 31 (1985), стр 78–105. Резюме-Compendex | Резюме-INSPEC | $Order Документ | MathSciNet

36. M.R. Garey и D.S. Johnson. Компьютеры и неподатливость: справочник к теории NP-законченности, Почетного гражданина, Сан-Франциско (1979).

37. L. Kleinrock. Сети коммуникации: стохастический поток сообщения и задержка, Дувр, Нью-Йорк (1964).

38. Kleinrock L. Системы организации очередей, vols. 1–2. Нью-Йорк: Wiley-межнаука; 1975–1976.

39. М. Dell'Amico, A. Lodi и F. Maffioli, Решение совокупной проблемы назначения с хорошо структурированным табу ищет на методе. Журнал Эвристики 5 (1999), стр 123–143. Резюме-Compendex | Резюме-INSPEC | $Order Документ | Полный Текст через CrossRef

40. R. Battiti и Г. Tecchiolli, реактивный запрещённый поиск. Журнал ORSA при Вычислении 6 2 (1994), стр 126–140. Резюме-INSPEC | $Order Документ

41. T.G. Crainic и М. Gendreau, Кооператив находит что-либо подобное запрещённому поиску capacitated сетевой дизайн. Журнал Эвристики 8 (2002), стр 601–627. Резюме-INSPEC | Резюме-Compendex | $Order Документ | Полный Текст через CrossRef

42. T. Trafalis и S. Kasap, роман metaheuristics приближается для непрерывной глобальной оптимизации. Журнал Глобальной Оптимизации 23 (2002), стр 171–190. Полный Текст через CrossRef

43. М Ericsson, M.G.C. Resende и после полудня. Pardalos, генетический алгоритм для веса, устанавливающего проблему в маршрутизации OSPF. Журнал Комбинаторной Оптимизации 6 (2002), стр 299–333. Резюме-INSPEC | Резюме-Compendex | $Order Документ | Полный Текст через CrossRef



		Этот Документ


			SummaryPlus
			Полный Текст + Ссылки
			Изображения ·Thumbnail
			PDF (259 K)



		Действия


			Процитированный
			Сохраните как Предупреждение Цитаты
			Почтовая Статья
			Экспортная Цитата

Запрещённый алгоритм поиска для маршрутизации и полной проблемы назначения в компьютерных сетях

Резюме

Схема Статьи